Which is appropriate to use fixed-effect or random effect statistical model while conducting meta-analyses?

Introduction:

Meta-analysis is the statistical analysis of data and an essential aspect of systematic reviews. Here, the study is conducted based on mathematical models. Meta-analyses are applicable for a number of purposes, including synthesizing data on the results of interventions and supporting evidence-based policy and practice. A meta-analysis is a tool with multiple applications in various fields like medicine, healthcare, pharmaceuticals, psychology, ecology, education, criminology and business (Borenstein 2021). The two most popular models used in conducting meta-analyses are fixed-effect and random-effect models. This review focuses on and compares both these models based on recent studies. 

Meta-analyses – different components:

A meta-analysis is a statistical method for combining quantitative data from various studies that address the same or similar research question (Schober 2020). A number of steps are involved in conducting a meta-analysis. These include – question framing, formation of search strategy, the search of literature database, selection of articles, data extraction, examination of quality of the articles, test for heterogeneity, estimation of summary effect, evaluation of the sources of heterogeneity, assessment of publication bias and finally, presentation of results (Wang 2021).

Fixed-effect and random-effect methods help in measuring the summary effect of a meta-analysis. Both these approaches are very distinctive. 

Fixed and random effect models:

In the fixed-effect model, it is assumed that there is one real effect that underpins all of the studies in the research, and that all variations in observed results are due to sampling error in the fixed-effect model. It is also known as the common-effect model. In this model, all variables that could affect the effect size is the same across all studies, and therefore the true effect size is the same across all studies(Borenstein 2021). The pooled or summary effect in a fixed-effect meta-analysis estimates this typical true effect size (Schober 2020). Two conditions must be satisfied in order for a fixed-effect model to be applied. To begin, one must be confident in the similarity of all studies included in the meta-analysis and that synthesizing the data is appropriate. Next, calculation of common-effect size is considered that is only applicable to the meta-analysis population (Spineli 2020a). Random effect models, on the other hand, presume a different underlying effect for each sample and treat this as a random source of variance (Wang 2021). In this model, It is often assumed that true effects are normally distributed, or they differ from study to study (Borenstein 2021).

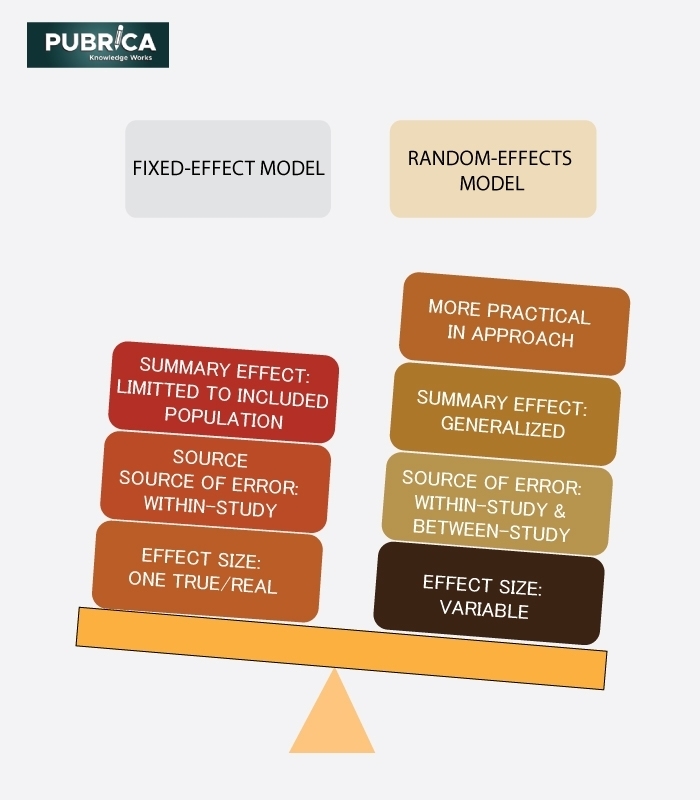
The comparison:

Both of these widely used meta-analysis models have their own set of limitations. When the heterogeneity of studies cannot be neglected, the common-effect model can produce misleading results. When the number of studies is small, the CI (confidence interval) for the mean effect based on the random-effect model can be too large to be helpful. Since a large portion of meta-analyses includes numbers of studies with non-negligible variability, these limitations are significant roadblocks in practice (Lin 2020). Another point to note is, as we compare the weighting schemes of these two models, we can observe that as we move from a fixed-effect to a random-effects model, larger studies tend to lose influence, and smaller studies tend to gain influence (Spineli 2020 *(a)).

Furthermore, the different assumptions for fixed-effect and random-effect models indicate different meanings of the variance (resulting in distinguished computations of the meta-analysis results due to varying weighting schemes) and the distinguished null hypothesis of no linear correlation determinations. The only source of error in a fixed-effect model is within-study variance and, the null hypothesis states that the typical true effect size is unrelated to the covariate of interest. Contrastingly in a random-effects model, both within-study and between-study variances are sources of error and, the null hypothesis states that the mean of the true effect size is unrelated to the covariate of interest (Spineli 2020 *(b)).

Conclusion:

To conclude, a fixed-effect model can only be applied if there are potential factors that indicate that the studies involved are identical for all intents and purposes (Borenstein 2007). However, implementation of the fixed-effect model is rarely possible in practice. The effect size varies from study to study in real-world synthesis. It is due to a variety of factors like differences in participant mixes and intervention implementation. As a result, a random-effects model appears to be sufficient and efficient in most meta-analyses (Spineli 2020 *(a)). 

Fig. 1: Comparison of fixed and random effect statistical models

The question of which model matches the distribution of effect sizes and takes into account the appropriate source(s) of error must be the sole consideration when choosing a model (Borenstein 2021). Finally, the best model to use depends highly on the type of study conducted and the nature of the goals that it wants to achieve.

References:

1. Borenstein, M., Hedges, L., & Rothstein, H. (2007). Meta-analysis: Fixed effect vs. random effects. Meta-analysis. Com.
2. Borenstein, M., Hedges, L. V., Higgins, J. P., & Rothstein, H. R. (2021). Introduction to meta-analysis. John Wiley & Sons.
3. Lin, E., Tong, T., Chen, Y., & Wang, Y. (2020). Fixed-effects model: the most convincing model for meta-analysis with few studies. arXiv preprint arXiv:2002.04211.
4. Schober, P., & Vetter, T. R. (2020). Meta-Analysis in Clinical Research. Anesthesia and analgesia, 131(4), 1090–1091.
5. Spinelii, L. M., & Pandis, N. (2020). The importance of careful selection between fixed-effect and random-effects models. American journal of orthodontics and dentofacial orthopedics, 157(3), 432-433. *(a)
6. Spineli, L. M., & Pandis, N. (2020). Fixed-effect versus random-effects model in meta-regression analysis. American journal of orthodontics and dentofacial orthopedics, 158(5), 770-772. *(b)
7. Wang, X. M., Zhang, X. R., Li, Z. H., Zhong, W. F., Yang, P., & Mao, C. (2021). A brief introduction of meta-analyses in clinical practice and research. The journal of gene medicine, e3312. Advance online publication.