In Brief

1. SEM are used meta-analytical model formulated for conducting Meta-analysis which is used to analyse structural relationships. SEM can be univariate, multivariate, and three-level meta-analysis
2. Structural equation model (SEM) in general optimized and fit by using OpenMx package
3. The routine analysis of batch mode either interactively or noninteractively can be analysed by R package. Using the graphical interface like R studio is convenient method for users to interfere the analysis.

A methodological tool used for comparing the data of the studies obtained between two groups was Meta- analysis. Multiple pairwise meta-analyses were used for comparing the data obtained from more than two groups. In recent, network meta-analysis was developed for analysing the data obtained from multiple group. SEM is one such method used for analysing longitudinal data. A collection of functions via., R statistical platform accessed by OpenMx package for conducting meta-analysis using SEM is the metaSEM package. Correlation and covariance matrices can be obtained using the SEM in this approach. Meta-analysis can be conducted by various unrelated programs for performing research in scientific and social studies. But the data analysis in computational studies using R is considered as a popular source for conducting statistical analysis. R is an open source platform compromises several packages. Among which MetaSEM along with OpenMx package is used for conducting meta-analysis in univariant, Multivariant and three level strategies. MetaSEM also uses two stage structural equation modelling (TSSEM) for correlating and studying covariance matrices in meta-analytic structural modelling.

SEM (Structural Equation Modelling)

The relation among measured variables and latent constructs in the aspect of structural can be analysed using SEM. It also possesses the techniques like path and factor analysis, regression and latent growth curve modelling for solving linear equations. It is a single analysis technique used for estimating interrelated dependence and multiple factors. Endo and exogenous variables can be used simultaneously in SEM. The approach of analysing relation between correlated traits, makes SEM a popular tool for analysing complex genetic traits. It also associates multiple variance and correlation between genetic phenotypes of interest. There are various software for analysing independent observations using SEM framework.

Structural Equation Modelling Based Meta-analysis

A hypothesis can be tested and fit with the multivariate technique using the SEM model. It is used for continuously analyse the multivariate distribution using the variable number observed. It is postulated that the model for the first which includes the vector of parameters that can be regression coefficients, error variances, factor loadings, and factor variances. The model is:

μ=μ(θ) and Σ=Σ(θ)

Where μ and Σ are the vector of mean population and covariance matrix. The most common method for estimating method in SEM is Maximum likelihood (ML) estimation method. The −2*log-likelihood for the th case is,

−2LLi(θ;yi)ML=pilog(2π)+log|Σi(θ)| + (yi−μi(θ))⊤Σi(θ)−1(yi−μi(θ))

here filtered variable numerical is represented by p_i, the mean vector implied model are ith case, μ_i(θ) and Σ_i(θ) and covariance matric implied in the model can be represented as ith case, respectively. The i in subscript represents the variation in mean vector and covariance matrix implied in the mean implied. It has the potential for handling the incomplete data in the log-likelihood function using estimation method used for maximum likelihood (M. W.-L. Cheung, 2015).

The minimized data of total sum of all −2LL_i represents the estimation of parameters. The inverse of Hessian matrix gives the details of estimates of parameter sampling covariance matrix of asymptotic sampling while being convergent. The square root element diagonal to covariance matrix of covariance matrix can be considered as the standard error. Nested model can be compared using the statistics of the likelihood ratio. The model fit and the significance of individual parameters can be tested (M. Cheung, 2015). MetaSEM can use various model for analysing the data.

Univariate Fixed-Effects Model

One effect size yi used meta-analysis in the ith study, yi can be any effect size, such as the odds ratio, raw mean difference, standardized mean difference, correlation coefficient, or its Fisher’s z transformed score. yi can be assumed to be normally distributed with a variance of vi while the sample sizes in the primary studies are reasonably large (M. Cheung, 2015).

Figure 1 Univariate Fixed-Effects Model

Univariate Random-Effects Model

The own specific study effect can be selected for the random-effects model in case of the variation in the expected population size. The model for the ith study is:

yi=βR+ui+ei,

Where β_R is the average population effect under the random-effects model, and Var(u_i) = τ² is the heterogeneity variance that has to be estimated. To fit the model in SEM, we may consider the following model implied moments:

μi(θ)=βR and Σi(θ)=τ2+vi.

Figure 2 Univariate Random-Effects Model

Univariate Mixed-Effects Model

The mixed-effects meta-analysis extends the random-effects meta-analysis by using study characteristics as predictors. Assuming that x_i is an (m + 1) × 1 vector of predictors including a constant of 1 where m is the number predictors in the ith study, the mixed-effects model is:

yi=x⊤iβ+ui+ei

where β is a a (m + 1) × 1 vector of regression coefficients including the intercept. To fit the model in SEM, we may use the following model implied conditional mean and variance:

μi(θ∣∣xi)=x⊤iβ and Σi(θ∣∣xi)=τ2+vi.

Figure 3 Univariate Mixed-Effects Model

Multivariate Meta-Analysis

To fit the multivariate mixed-effects meta-analysis in SEM, we use the following model implied conditional mean vector and covariance matrix. Summarizing the primary outcome using the  single effect size inn complicated research question is not sufficient. Hence, nmltiple effect sizes are required to quantify the effect of the studies. A total of p effect sizes was assumed with m predictors in k studies.  In different effect sizes, p_i can be assumed as effect sizes in the ith study. The model for the multivariate mixed-effects meta-analysis in the ith study is:

yi=Bixi+Ziui+ei,

Where y_i is a p_i × 1 vector of effect sizes, B_i is a p_i × (m + 1) matrix of regression coefficients including the intercepts, x_i is a (m + 1) × 1 matrix of predictors including 1 in the first column, Z_i is a p_i × p filter matrix selecting the effect sizes that are present, u_i is a p × 1 study-specific random effects, and e_i is a p_i × 1 sampling error.

We assume that Var(e_i) = V_i is known in the ith study and that Var(u_i) = T² is the variance component of the between-study heterogeneity that has to be estimated. Since x_i is a design matrix, missing value is not allowed in x_i. When there are missing values in x_i, the whole study will be deleted before the analysis is conducted M. Cheung,(2013). The −2LL of the above model is:

−2LLi(B,T2;yi)ML= pi∗log(2π)+log∣∣ZiT2Z⊤i+Vi∣∣+ (yi−Bixi)⊤(ZiT2Z⊤i+Vi)−1(yi−Bixi).

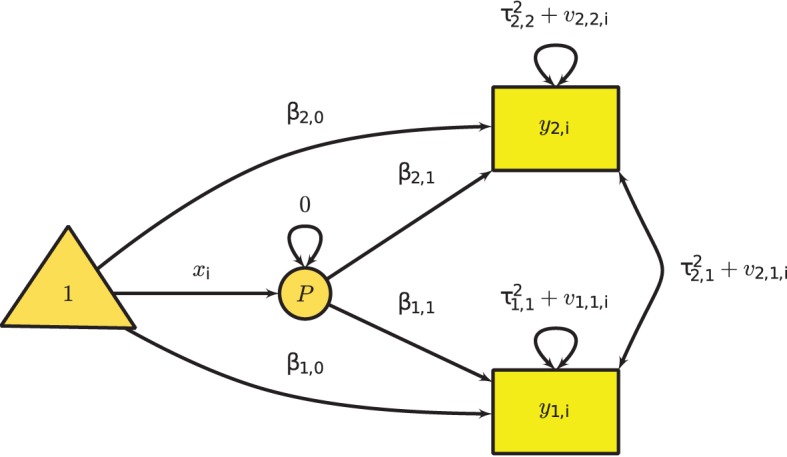
Figure 4 Multivariate Meta-Analysis

References:

1. Cheung, M. (2013). Multivariate Meta-Analysis as Structural Equation Models. Structural Equation Modeling: A Multidisciplinary Journal, 20(3), 429–454. https://doi.org/10.1080/10705511.2013.797827
2. Cheung, M. (2015). metaSEM: an R package for meta-analysis using structural equation modeling. Frontiers in Psychology, 5. https://doi.org/10.3389/fpsyg.2014.01521
3. Cheung, M. W.-L. (2015). metaSEM: An R package for meta-analysis using structural equation modeling. Frontiers in Psychology, 5, 1521. Retrieved from https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4283449/#__ffn_sectitle