Mean and Mean difference are the two key statistical measures used in the statistical analysis. Both are essential for meta-analysis as well. Mean and Mean difference are used for the interpretation of a large set of values into a single number which explains the heterogeneity and variation among the individual values. However, one of a common challenge in meta-analysis is the unavailability of this data (mean and standard deviation).

Q & A Forum

Meta Analysis

Q: What is the difference between Mean and Mean difference in meta-analysis?

Editorial Guidance on Plagiarism_ Upholding Research Integrity

Introduction

Mean and Mean difference are the two key statistical measures used in the statistical analysis. Both are essential for meta-analysis as well. Mean and Mean difference are used for the interpretation of a large set of values into a single number which explains the heterogeneity and variation among the individual values. However, one of a common challenge in meta-analysis is the unavailability of this data (mean and standard deviation).

What is Mean in Meta Analyses:

Mean is the average value that is obtained by pooled estimation of group of data with same measurement units. 

For example, assume that 6 different studies presented weight gain in 16 weeks with clozapine. The weight gain for each study is 6 kg, 5 kg, 4 kg, 4 kg, 7 kg, 5 kg. if we calculate the average of the six studies, we get 5.16 as mean value. From this pooled estimate, we conclude that on average patients gain 5.16 kg weight after treatment with clozapine for 16 weeks.  

In Meta-analysis the average data is calculated in the same way, but studies with less standard deviation gets more weightage than the higher standard deviation. The precision of the mean value is estimated by standard error of the mean. The standard error of the mean is lesser when the standard deviation is less. The smaller the SEM the higher the precision of the mean value.

There is a circumstance where descriptive statistics are available but no mean and SD in the individual study, what I should do?

What is Mean difference in the meta-analysis?

Mean difference is the difference between mean of two variables in the same outcome.
Context of Mean difference Explained, Compiled by Pubrica Medical Experts.
Figure 1. Context of Mean difference Explained, Compiled by Pubrica Medical Experts.

In Meta-analysis the average data is calculated in the same way, but studies with less standard deviation gets more weightage than the higher standard deviation. The precision of the mean value is estimated by standard error of the mean. The standard error of the mean is lesser when the standard deviation is less. The smaller the SEM the higher the precision of the mean value.

There is a circumstance where descriptive statistics are available but no mean and SD in the individual study, what I should do?

Connect with us to explore how we can support you in maintaining academic integrity and enhancing the visibility of your research across the world!

Contact Us

What is Standardized mean difference?

The standardized mean difference (SMD) is used as a summary statistic in meta-analysis when different studies evaluate the same outcome but employ different measurement methods (e.g., various psychometric scales to assess depression). In such cases, standardizing the results onto a common scale is essential before they can be pooled together. The SMD represents the magnitude of the intervention effect in each study relative to the observed variability within that study. Importantly, the actual intervention effect is reflected as a difference in means rather than the mean of differences.

Standardized mean difference is used when we are measuring the outcome from all the studies in different units in meta-analysis. This is also called effect size.
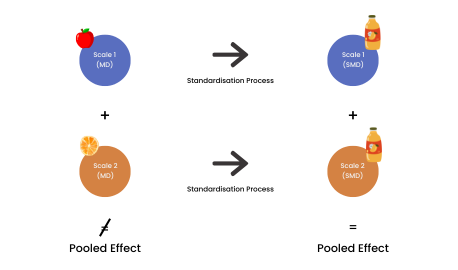
Mean & Mean difference
Figure 2. Standard mean difference for different units – Explanation Figure
For instance, if studies assess depression using different measurement units, the results must first be standardized to a uniform scale. This calculation measures the size of the effect across all studies relative to their standard deviation. [2]
Example: A study evaluating the efficacy of folic acid supplementation on cognitive function presents the effect using Full Scale IQ (FSIQ). The FSIQ for the intervention group and control group is 109.11 and 107.40, respectively, at baseline, and 118.41 and 107.41 after 24 months of treatment. The standard deviation (SD) is 6.71 for the intervention group and 9.37 for the control group.
First, calculate the pooled standard deviation using the appropriate formula.

Table.1   Data extracted from Ma et al [3] 

Measurement  

Groups 

Cases 

Baseline 

24 months 

Full scale IQ 

Intervention 

90 

109.11 ± 7.18 

118.41 ± 6.71 

control 

90 

107.40 ± 11.47 

107.41 ± 9.37 

data extraction
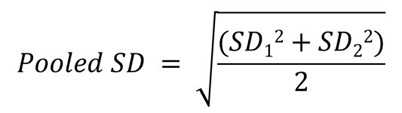
pooled Sd

Apply the values in this formula 

                                                       = √6.71+9.37/2= √8.04 = 2.83 

Pooled standard deviation= 2.83 

Now we can insert all the values in standard mean difference formula, 

SMD= Difference between clozapine and haloperidol group/Pooled standard deviation 

SMD= 9.3-0.01/2.83 = 3.28 

Finally, we get the SMD value 3.28 for this study. In the same way we can calculate SMD for all the studies and compare them in meta-analysis. [3] 

References: 

  1. Andrade C. Mean difference, standardized mean difference (SMD) and their use in meta-analysis: as simple as it gets. J Clin Psychiatry. 2020;81(5):20f13681. doi:10.4088/JCP.20f13681. 
  2. https://handbook-5-1.cochrane.org/chapter_9/9_2_3_2_the_standardized_mean_difference.htm 
  3. Ma F, Li Q, Zhou X, et al. Effects of folic acid supplementation on cognitive function and Aβ-related biomarkers in mild cognitive impairment: a randomized controlled trial. Eur J Nutr. 2019;58(1):345-356. doi:10.1007/s00394-017-1598-5 

This will close in 0 seconds